Classical Mechanics

10/22/2007

Stanford class with Leonard Susskind.

Conservation of Energy and Momentum

In what follows the meaning of the index is that it indexes the three space coordinates.

The kinetic energy:

Take the derivative of the kinetic energy. Use the chain rule.

Substitute

to get

Take the time derivative of the potential.

Define the total energy.

Take the time derivative.

Define the applied force to be the space derivative of the potential.

then

Therefore, conservation of energy.

Change the meaning of the index so that it now indicates the i^th particle.

Assume that the force on a particle is the sum of the forces applied by the other particles.

Assume that the forces are “equal and opposite”.

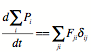
Since

then

Therefore, conservation of momentum.

Principle of Least Action

The problem is to minimize the function .

at the minimum or stationary point

also

at the minimum

F=ma is local. However, the Principle of Least Action is global. Need endpoints specified, and not initial conditions.

variable speed of light?

The total time is

Consider the Action “A” and the Lagrangian “L”.

which implies

when minimized.

Sometimes the Action is labeled with “I” or “S”. In general

The Principle of Least Action is