Classical Mechanics

11/05/2007

Stanford class with Leonard Susskind.

The Euler-Lagrange Equations

Define the canonical momentum

The Euler-Lagrange equations become

Example:

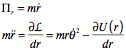
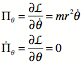
Function minimization

Consider the problem of minimizing the function with respect to the . The variation of the function vanishes at the minimum (or extremum).

Use the chain rule.

Implies that

since the variations are arbitrary.

The variation of the action vanishes at the extremum.

Implies a symmetry. The action is

Perform integration by parts.

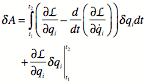
Start with the assumption that the Euler-Lagrange are satisfied,

which causes the first integral to vanish. Assume that variation is a symmetry, so vanishes.

There is immediately a conservation law.

or

so that is conserved as an Emily Noether current.

Example: invariant under a displacement

Given a number of particles indexed by . Consider a displacement in the x-direction.

constant

Momentum in the x direction is constant.

Example: rotational symmetry

The variation due to an infinitesimal rotation is

Calculate the Noether charge.

The conserved quantity is

therefore for particle

Sum over all particles.

Consequence of time invariance

Time invariance involves a displacement in the time coordinate.

then

or

Assume the displaced trajectory is also a solution of the equations of motion.

Treat the endpoints separately. Assume the variation of the action vanishes.

Perform an integration by parts.

Assume and that the system is “on trajectory” so that the Euler-Lagrange equations are satisfied.

then

Substitute

then

or

Divide out the epsilon and since the difference is zero

is conserved

Hamiltonian

The Hamiltonian is

Example:

then

and

Another student had the book: “Basic Theoretical Physics” by Krey, Owen. Published by Springer-Verlag.