Classical Mechanics

11/12/2007

Stanford class with Leonard Susskind.

Example: Simple pendulum

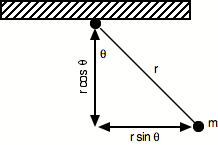
Velocity:

Kinetic energy:

Potential energy:

Potential energy is at a minimum when .

The Lagrangian is:

Angular momentum is:

The Euler-Lagrange equations are

is constant, so the equations of motion are

Calculate the Hamiltonian

The Hamiltonian is the total energy.

Specifically, for the pendulum,

Substituting

Example: the double pendulum

The double pendulum has two “bob’s”, in this case “Bob” and “Herman”.

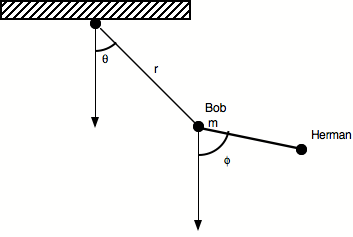
Kinetic energy of Bob:

Velocity of Herman:

Add the velocity of Herman with respect to Bob to get the velocity of Herman.

Kinetic energy of Herman:

Sum of the kinetic energies of Bob and Herman is:

The sum of the potential energies of Bob and Herman is:

The Lagrangian becomes:

No conserved quantity under the force of gravity.

Conserved quantities with no gravity

However, investigate case (no gravity):

Noether symmetry

then

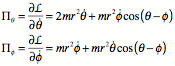
Total angular momentum should be conserved.

Calculate the equation of motion for .

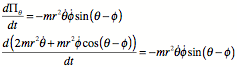
Example: simple harmonic motion

Approximate:

Substitute into the Lagrangian for simple harmonic motion, and drop the constant term.

Use the variable “x”. Consider a spring.

x=0 at equilibrium.

The potential energy is the work done against the spring from equilibrium.

“k” is the spring constant.

The force exerted by the spring is (Hooke’s Law):

The Lagrangian for simple harmonic motion is:

The Euler-Lagrange equations are (F=ma)

Let

then

Substitute:

The Sine is also a solution. In general, the solution to this second order equation is:

A specific solution requires the initial position and velocity.

Another way of putting the solution

where at .

Construct the Hamiltonian.

is conserved.

Consider the Hamiltonian formulation

Instead of use . Solve for in terms of .

Hamiltonian mechanics is symmetric between x and p.

Phase space

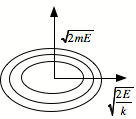
is conserved.

Therefore, the shape of the trajectory in phase space is that of an ellipse. is the square of the semi-major and minor axis.

when

What is the period of the orbit? It is the frequency . All the elliptical orbits are repeated with frequency .

Phase space is fundamental. An orbit in phase space is a contour of constant energy. Area in phase space is preserved in time. In quantum mechanics this is “unitarity” or conservation of probability.