Classical Mechanics

11/19/2007

Stanford class with Leonard Susskind.

Hamiltonian mechanics

Hamiltonian:

· determines the evolution of a system

· phase space states are indicated by points

· trajectories could be closed cycles and multiple cycles

· each cycle represents a conservation law

Cycles in phase space

Cycles don’t run into each other. This can be viewed as information conservation. No phase space points are gained or lost. Example

Hamilton’s Equations

N 2^nd order equations imply 2N 1^st order equations.

N equations

Define:

then

so 2N first order equations with the variables . This is a Legendre transformation.

is a canonical momentum. Hamilton’s equations describe how a point moves in phase space.

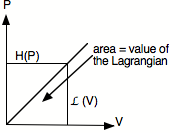
Consider V (a velocity) and P (a momentum) which are single valued functions of each other. The graph looks like

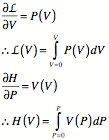
now construct

represent a small change as:

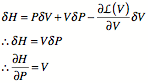
Suppose many V’s.

now construct

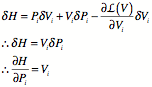
How we do mechanics with a Lagrangian.

Repetition, but in the language of Mechanics.

Let

then

from previous definitions

“q”, the coordinate goes along as a parameter – passive.

Since

then

Take partials.

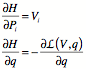
Given the Euler-Lagrange equation

then

where

Velocity is eliminated in favor of position and momentum.

Hamilton’s equations defines modern classical mechanics.

Recapitulate, an 2^nd order set of equations can be put into Hamiltonian form.

Knowing allows calculation of velocity in phase space.

Friction appears only when some coordinates are ignored. Can’t write a system with friction in Hamiltonian form.

Example of Hamiltonian methods.

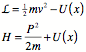
Check Hamilton’s equations:

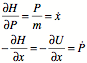
Hamilton’s equations establish the relation between velocity and momentum and gives the dynamics of the momentum.

Energy Conservation

Find the total time derivative of the Hamiltonian by using the chain rule.

Substitute Hamilton’s equations

The Hamiltonian is constant in time, and so conserved, as long as there is no explicit appearance of time in the Hamiltonian.

A trajectory in phase space stays on a surface o constant energy. The density of points in phase space doesn’t change, so that the phase points behave as an incompressible fluid.

Example: Washboard potential

For large energies the motion is translational. For small energies, it is simple harmonic around a low point.

Assume all quantities are functions of P and q. Calculate the derivative of an arbitrary quantity A(P,q).

Define the Poisson bracket.

Therefore

Check it.

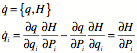
Similarly

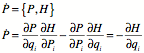
If there is explicit appearance of time then