Classical Mechanics
11/26/2007
Stanford
class with Leonard Susskind.
We study Liouville’s theorem tonight. We’ll prove Liouville’s theorem from Hamilton’s equations. Liouville’s theorem can be thought of as information conservation.
The laws of mechanics are synonymous with a specification for state transition.
A flow through phase space doesn’t condense, it moves as an incompressible fluid. No divergence or convergence. Forbidden.
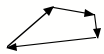
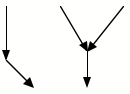 Not allowed in
Classical Mechanics
Not allowed in
Classical Mechanics
Ignored degrees of freedom, such as friction can result in
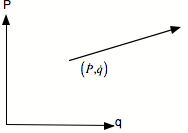
multiple paths to the same final state. A point in phase space is ![]() while it’s
velocity is
while it’s
velocity is ![]() .
.
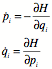
In one dimension incompressible motion implies a constant velocity.
Consider two dimensions.
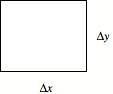
The density of points must not change, so the number of points inside the rectangle must be constant.
Points per second leaving the four faces must sum to zero.
For a given wall:
![]() gives the points
per second with velocity crossing a wall with velocity
gives the points
per second with velocity crossing a wall with velocity ![]() . This can be written as
. This can be written as
![]()
The quantity
![]()
gives the difference in horizontal output vs. input between the left and right walls.
Now do the same for the y-direction.
![]()
![]() vanishes for
incompressible flow
vanishes for
incompressible flow
then divide by ![]()
![]()
for incompressible flow.
Calculate divergence of phase space velocity field according to Hamilton’s equations.
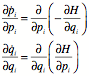
so that the sum is zero for incompressible fluids!
![]()
Liouville’s theorem
No conservation of distance, only area.
Example (one dimensions):
![]() , then
, then ![]()
Consider coordinate transformations. (Should use x rather than y).
![]()
![]()
then ![]()
![]()
![]()
Therefore
![]()
The product is constant
![]()
Plank’s constant represents area in phase space. Canonical transformations, we’ll discuss later. The area of phase space has the units of ??. Area has an invariant meaning.
chaotic systems
coarse graining, means area increases with time.
finite precision in an experiment implies coarse graining.
implies 2nd law of Thermodynamics.
Volume of phase space is a measure of Entropy.
Entropy = log Volume
Velocity dependent forces: magnetic fields
![]() is
the magnetic field.
is
the magnetic field.
![]() force on a charge
force on a charge ![]() due to magnetic
field.
due to magnetic
field. ![]() is the velocity.
is the velocity.
![]()
![]()
![]()
Need a vector potential in order to write a Lagrangian or Hamiltonian.
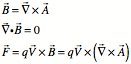
e.g. ![]()
This is the magnetic force equivalent
to ![]() .
.
We want to discover the Lagrangian and Hamiltonian
![]()
The units for the Action integral are momentum * x or energy * time.
![]()
since ![]()
Therefore
![]()
or
![]()
Take this Lagrangian to prove
![]()
The canonical momentum is:
![]()
or, in index notation,
![]()
The portion of the canonical
momentum equal to ![]() is sometimes
called “mechanical” momentum.
is sometimes
called “mechanical” momentum.
![]()
or
![]()
then
![]()
Substitute on the left.
![]()
![]()
or
![]()
The Hamiltonian is
![]()
for any Lagrangian. Investigate the Lagrangian:
![]()
Need momenta, not velocity, in Hamilton’s equations.
![]()
Substitute for ![]()
![]()
Substitute into the Hamiltonian.
![]()
There is no ![]() , therefore the magnetic field does no work.
, therefore the magnetic field does no work.
Solve for ![]() in momentum
in momentum
![]()
then
![]()
Use this expression for the Hamilton’s equations.
![]() is the canonical
momentum.
is the canonical
momentum.
Exercise:
verify ![]() using Hamilton’s
equations.
using Hamilton’s
equations.