Classical Mechanics

12/17/2007

Stanford class with Leonard Susskind.

Introductory discussion:

Symmetries

Conservation of area in phase space

points move but are conserved

implies information conservation

Hamilton’s equations show that volume is conserved. We proved this: Liouville’s Theorem.

Motion in an Electric Field

e.g. Hall Effect

Equation of motion: 2^nd order differential equation

Principle of Least Action underlies Lagrangian and Hamiltonian methods

Lagrangian:

Hamiltonian: flow in phase space

Liouville’s theorem

Electromagnetic equation of motion:

Magnetic force is perpendicular to velocity, so that it does no work.

Define vector potential:

implies (no magnetic charge)

(electric charge)

Any field with zero divergence can be written as the curl of a vector field.

Define: where is a scalar potential (voltage)

The force remains where the potential energy is .

It can be proven that a Least Action formulation requires the vector potential.

Equation of motion in an electromagnetic field

Principle of Least Action for the electromagnetic field

or

It appears as if is the “time” component of a 4-potential. Write the vector potential term as

then

or

so that in general, the Lagrangian for motion in an electromagnetic field is:

Gauge invariance

Note that the curl of is unchanged with the addition of a term

since

Therefore, curl free.

Extract the equation of motion from the Lagrangian

is the canonical momentum and is not gauge invariant. The equation of motion is:

The left hand side is:

Assume no explicit dependency on the time .

Now the right side is

Several terms cancel.

or

Example: constant

Investigate 3 gauges:

In general, the Lagrangian for motion in an electromagnetic field is:

The Lagrangian for the example in one of the gauges is:

The Lagrangian is invariant under because only the derivative of enters. is conserved.

(if )

In a different gauge.

which is invariant under . Therefore

(if )

Therefore, together,

Notice that the two different gauges can be used simultaneously!

The solution will look like

and

Two different gauges are used.

1.

2.

Two gauges:

1.

2.

Substitute, then note that and are conserved. xxxx

also

Therefore the center of the circle does not move.

Example: Add an electric field acting in the x-direction.

then

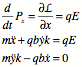
Investigate particular solutions where .

Then and which is the Hall Effect.

This is similar math for a gyroscope.

Homework problem:

work out Hamiltonian for a charged particle.

Work out our example for Hall Effect in Hamiltonian formulation

Poisson Brackets:

Consider the Poisson bracket of an arbitrary function of position and momentum .

How does vary in time along a trajectory. Assume has no explicit time dependence.

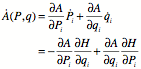
Poisson brackets are defined as

Then

Example: if is constant, then and A commutes with H.

Hamilton’s equations are a consequence of this formulation.

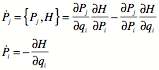
and similarly .

Axiomatic structure of Poisson Brackets

Axiom

therefore

and

Investigate or (the Kronecker delta)

Symplectic structure: swap q and P

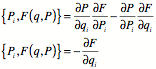
Similarly,

In general,

Need more axioms to systematize Poisson Brackets.

Need one more axiom concerning products.

Use Leibnitz product rule for the derivative.

then

These axioms are sufficient to calculate any Poisson bracket that is a polynomial function, and it can be extended to non-polynomial functions.

These axioms form a completely determined system.

Heisenberg and Dirac used Poisson brackets in quantum mechanics.