Classical Mechanics

12/20/2007

Stanford class with Leonard Susskind.

 

Goal:  create a body of amateur Physicists. people are interested in physics, but not employed by a University. For people who don’t otherwise have access to a graduate course.

 

Poisson brackets formulation were used to describe phase space and flow in phase space.

 

Imagine a rotation of a system. Coordinates are . The rotation transformation may mix the p’s and q’s.

 

Axiomatic structure of Poisson Brackets

                    Antisymmetric

               Linear

              Product rule

 

           

 (the Kronecker delta)

 

             and

 

The momentum is related to the partial derivative.

           

Proof:

            • 1st show that the relation is true when  is a polynomial.

Start with a constant term. Any constant will do.

             by product rule

           

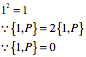
Now try 1st power of .

           

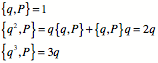
The pattern is that of a derivative. The proof is by mathematical induction.

           

and similarly

           

The time derivative along a trajectory

as before,

           

Example:

           

then

           

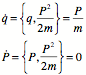
Canonical Transformations of Poisson Brackets

Question:  what are the allowable transformations that preserve the Poisson Bracket properties?

 

Example of a transformation.

             does not preserve properties since ?

However

             does preserve the properties.

 

Example:  Rotation.

We need to check only  since  by antisymmetry!

           

Therefore the structure is preserved.

 

Canonical transformations keep the relations unchanged.

 

Investigate an infinitesimal transformation. (suppress indices)

           

Drop infinitesimal quadratic terms.

           

It is necessary and sufficient that the following be true in order to maintain the Poisson Bracket structure:

           

Assume a generator function . Now substitute into a canonical transformation.

           

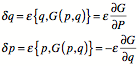
Always defines a canonical transformation.

           

So  is also a generator of another flow, another canonical transformation.

           

to get

           

therefore since

           

then

           

 

 

Consider canonical transformations that do not change the energy. That transformation is a symmetry.

 

Consider the time derivative of

           

Don’t know where this goes:

           

 

If the energy is not changed, then

              Generator commutes with the Hamiltonian so that  is conserved.

           

 

Example:  A canonical transformation (a rotation). Let

           

Let

           

 

           

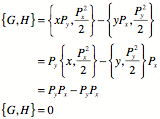
Therefore  is conserved under the rotation.

 

Make up a new system. Let

           

then

           

Therefore, circular motion.

Example:

           

then

           

 

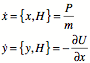
Homework:  Prepare for Quantum Mechanics next semester. Look at iTunes “Quantum Entanglement, the Logic of Discrete Systems”.

 

The end of the semester.