Special Relativity and Field Theory
4/14/2008
Stanford class
with Leonard Susskind. Lecture 1.
Inertial reference frames
Inertial reference frames are:
not accelerated
F=ma is valid
laws of physics are the same in any inertial reference frame
However, Maxwell’s equations did not predict constant velocity of light. For details look online at Stanford iTunes from about a year ago:
iTunes U/Stanford/Science and Technology/Modern Theoretical Physics – Fall 2006
Brief review of Special Relativity
Consider two inertial frames moving with respect to each other in the (x,t) plane. Coordinates in one frame transform to the other via a Galilean rotation.
Use ![]() to have uniform
units for all coordinates. Makes sense in the same way that x,y,z coordinates
should use the same units.
to have uniform
units for all coordinates. Makes sense in the same way that x,y,z coordinates
should use the same units.
A Galilean transformation assumes that time is universal and has the same value in all inertial systems. Consider the path of light in the (x,t) plane,
![]()
According to the transformation equations, equation ,
![]()
then
![]()
This transformation rule contradicts the Michelson-Morley experiment which demonstrated that the velocity of light is constant.
Circular Trig
Consider a rotation in the (x,y) plane.
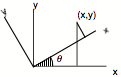
![]()
where
![]()
so that
![]()
then ![]()
and 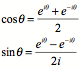
Notice that the distance is invariant under the transformation above
![]()
then ![]()
The Galilean transformation works for small velocities. According to Newton, the speed of light is large, but a constant in every inertial reference frame, counter to the Michelson-Morley experiment. Recall that in the year of the experiment 1887 no one had traveled 100 miles an hour and lived to tell the tale.
Hyperbolic Trig
Let ![]() . The coordinates for light allow two possibilities
(directions),
. The coordinates for light allow two possibilities
(directions),
![]()
Both directions are allowed as roots to the quadratic equation
![]()
This equation is necessary and sufficient for the constancy of the speed of light. This equation applies only for the speed of light.
The problem is now to find a transformation that leaves the velocity of light invariant.
Generalize the problem to any velocity, not just the velocity of light, so drop the condition of zero value and state the invariance.
![]()
Invariance requires the use of hyperbolic functions rather
than circular functions. Replace ![]() with
with ![]() .
.
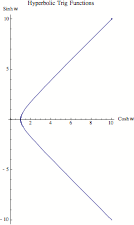 Define
Define 
then
![]()
Compare the ranges of ![]() and
and ![]() .
.
![]()
Guess the following transformation (Lorentz transformation)
![]()
Verify the expected invariant.
![]()
The “angle” parameter ![]() depends upon the
velocity between the two frames.
depends upon the
velocity between the two frames. ![]() in both frames
so that
in both frames
so that
![]()
Maxwell was aware that his equation had a rest frame where light went the same speed left and right. Maxwell assumed that we were approximately at rest with respect to the Ether. He assumed that the Ether was necessary.
The Michelson-Morley experiment showed constancy for the velocity of light in Earth’s orbit in any direction.
Find the interpretation of the parameter ![]() .
.
![]() after
transformation
after
transformation
![]()
therefore
![]()
Invert to find ![]() in terms of v.
Start the inversion procedure by first squaring both sides of the equation.
in terms of v.
Start the inversion procedure by first squaring both sides of the equation.
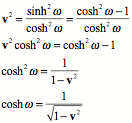
From above
![]()
Therefore ![]()
Now eliminate ![]() for v.
for v.
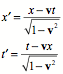
Restore the velocity of light to the equations.
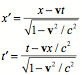
Exercise: calculate compounding velocities. Hint, add the hyperbolic angles, not the velocities.
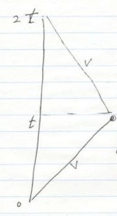
![]() is the distance
along the hyperbola.
is the distance
along the hyperbola.
The Lorentz transformation reduces to Newton’s velocity addition for small velocities.
Investigate time transformation.
![]() therefore, no
agreement as to simultaneity.
therefore, no
agreement as to simultaneity.
Substitute ![]()
to solve the inverse problem.
Consider the differential distance.
![]()
![]() is independent of
(invariant under) a rotation of the axis.
is independent of
(invariant under) a rotation of the axis.
Consider the hyperbolic
distance element. ![]() is the proper
time.
is the proper
time.
![]()
is invariant under a
Lorentz transformation and is independent of ![]() .
.
The proper time elapsed does not depend upon the choice of coordinates and so is an invariant under a Lorentz transformation. Proper time is the time an observer measures with a clock traveling with the observer.

The twin paradox: see other lectures.
The shortest path with the hyperbolic distance element is not the same as a straight line with a circular distance element.